초코chip의 코딩 생활

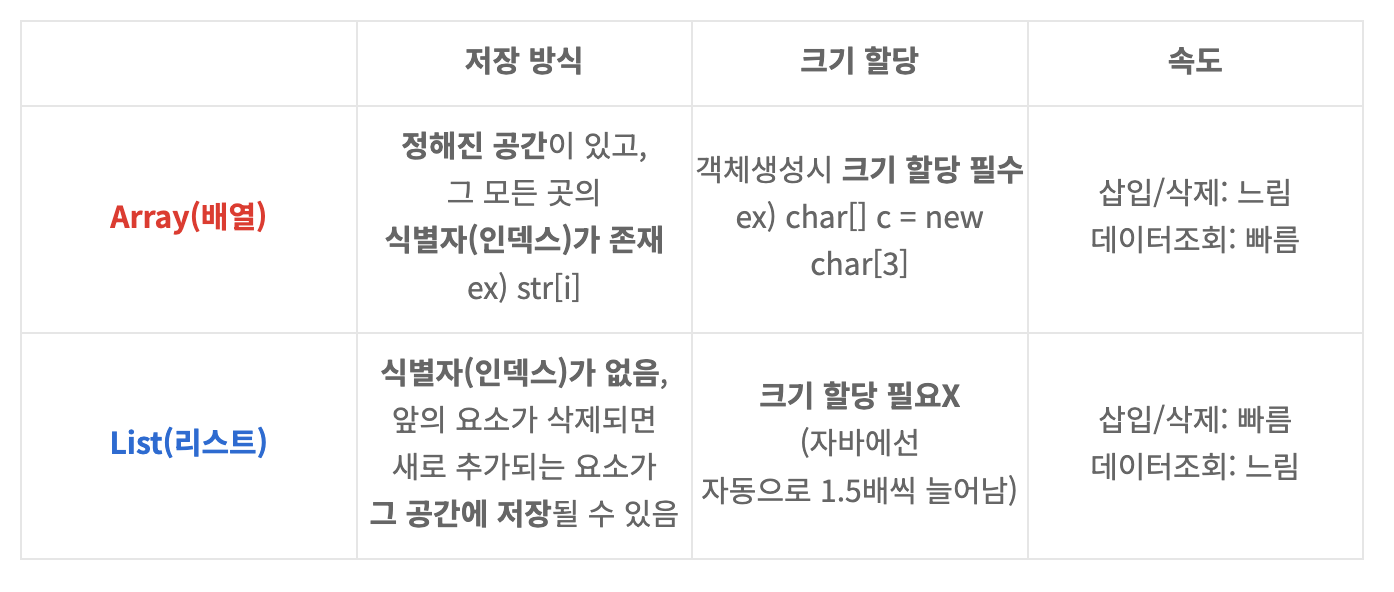
개념 오로지 기본 타입 말고 래퍼 타입만 사용 가능 값 접근(읽기): O(1) - 인덱스를 사용하여 바로 접근 가능 값 삭제/삽입: O(n) - 주변에 있는 값들을 옮겨주는 오버헤드 발생. 삭제 시 뒤의 원소들을 앞으로 당김, 삽입 시 기존 원소들을 뒤로 밀어냄 ArrayList 연산 종류 정리 생성 값 접근(읽기): list.get(1); 값 삽입, 삭제: list.add(); list.remove(); 리스트 크기: list.size() 리스트 최대,최소: Collections.max(list), Collections.min(list) 리스트 전체 초기화: Collections.fill(list, 값) 리스트 전체 출력: list.toString() 리스트 정렬: Collections.sort(lis..

개념 값 접근(읽기): O(1) - 인덱스를 사용하여 바로 접근 가능 값 삭제/삽입: O(n) - 주변에 있는 값들을 옮겨주는 오버헤드 발생 일반 배열 연산 종류 정리 생성 값 접근(읽기) 값 삽입, 삭제: 일반 배열로 감히 삽입,삭제를 할 생각하지 마라 배열 길이: arr.length 배열 최대,최소: Arrays.stream(arr).max().orElse(-1); 배열 전체 초기화: Arrays.fill(arr,1); 베열 전체 출력: Arrays.toString(arr) 배열 정렬: Arrays.sort(arr) 배열 생성 //배열 선언 int[] test = new int[n]; //배열 선언 및 초기화 int[] test = {1,2,3}; 배열 길이 int[] arr = new int[n];..

준비 public 클래스 이름 = Main 입/출력 = 표준 입출력 사용 입력: Scanner 객체 사용 출력: System.out.print 사용

배경 자바 언어를 사용하여 코딩하다보면, 때때로 (x, y) 형태의 데이터를 리스트에 저장해야 하는 경우가 발생 파이썬에서는 이런 작업이 쉽게 처리되지만, 자바에서는 약간 다른 접근 방식이 필요 따라서 자바 환경에서 해당 작업을 수행하는 방법을 정리하였음. 사용법 [ ] 배열 사용법 언제 가능?: x,y 값이 동일한 자료형인 경우에 사용 가능 장점: 별도의 코드 작성 없이 빠르고 간편하게 사용 가능 단점: x,y값에 대한 접근을 오로지 인덱스로만 해야해서 인덱스 의미를 잘 기억해야함 [ ] 배열을 삽입 하는 방법 Stack stack = new Stack(); //값 삽입 stack.push(new int[] {1, 3}); //값 조회 int[] node = stack.peek(); node[0]; /..

트리 개념 정의: 데이터를 계층적인 구조로 표현할 때 사용하는 자료구조 용어 루트 노드(root node): 부모가 없는 최상위 노드 단말 노드(leaf node): 자식이 없는 노드 크기(size): 트리의 모든 노드 개수(N) 기본적으로 트리 크기가 N이면 간선은 N-1개 깊이(depth): 루트 노드로부터 거리 높이(height): 깊이 중 최댓값 차수(degree): 각 노드의 자식 (간선) 개수 이진 탐색 트리(Binary Search Tree) 개념 정의: 이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조 특징: 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드 탐색 진행 흐름 시간복잡도: O(logN) 단, 트리 높이가 균등할때만 그럼 방법 if target 값이면 탐색..

기본편 개념 정의: 두 노드의 공통된 조상 중 가장 가까운 조상을 찾는 문제 동작 과정: 모든 노드에 대한 깊이(depth) 계산 최소 공통 조상을 찾을 두 노드를 확인 - LCA(a,b) 연산에 대하여 아래 과정을 반복 먼저 두 노드의 깊이(depth)가 동일하도록 거슬러 올라감 이후 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라감 시간 복잡도: O(N) - 매 쿼리마다 부모 방향으로 거슬러 올라가기 때문에 언제 사용?: m번의 LCA연산으로 총 O(MN) 시간 복잡도가 괜찮을 경우 메모리 여유가 없을 경우 구현 //n: 노드 개수, m: LCA연산 횟수 static int n, m; static int[] parent = new int[n+1]; // 부모 노드에 대한 정보 s..

개념 정의: 사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스리지 않도록 순서대로 나열하는 것 즉, DAG(Direct Acyclic Graph): 순환하지 않는 방향 그래프에 대해서만 가능 시간 복잡도: O(V + E) - 노드 개수(V), 간선 개수(E) 동작과정 요약 진입차수가 0인 모든 노드를 큐에 삽입 큐가 빌 때까지 아래 과정 반복 큐에서 원소를 꺼내 해당 노드에서 나가는 간선 그래프에서 제거 새롭게 집입차수가 0이 된 노드를 큐에 삽입 최종적으로 각 노드가 큐에 들어온 순서가 위상 정렬을 수행한 결과 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재 그래프 기본 개념 집입차수(Indegree): 특정 노드로 들어오는 간선 개수 진출차수(Outdegree): 특정 노드에서 나가는 간선..

서로소 집합 자료구조 서로소 집합 정의: 공통 원소가 없는 두 집합 예시) 서로소o: {1,2} {3,4} 서로소x: {1,2} {2,3} 서로소 집합 자료구조 정의: 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하는 자료구조 2가지 연산 지원 합집합(Union): 2개의 집합을 하나의 집합으로 합치는 연산 찾기(Find): 특정 원소가 속한 집합이 어떤 집합인지 알려주는 연산 합집합 연산을 통해, 노드 A와 B를 연결 A와 B의 루트 노드인 A`과 B`을 찾기 A`과 B`을 부모 노드로 설정 모든 합집합 연산을 처리할때까지 1번 연산 반복 진행 흐름 서로소 집합을 합치는 과정은 다음과 같이 진행된다. 예시) if 노드가 1~6번까지 존재하고, 4가지 합치는 연산이 존재하는 경우 1. 부모 테이블..

개념 최단 거리 문제 종류 모든 간선이 양수인 경우 - 다익스트라 알고리즘 음수 간선이 있는 경우 - 벨만 포드 알고리즘 음수 간선 순환이 없는 경우 - 다익스트라 O 음수 간선 순환이 있는 경우 - 다익스트라 X 벨만 포드 알고리즘 시간 복잡도: O(VE) - 다익스트라 알고리즘에 비해 느림 동작과정 간단 요약 출발 노드 설정 & 최단 거리 테이블 초기화 아래 과정을 N-1번 반복 전체 간선 E개를 하나씩 확인 ( 다익스트라는 특정 노드에 붙어있는 간선만 확인함 ) 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신 만약, 음수 간선 순환이 발생하는지 체크하고 싶다면, N-1 반복을 다시 한 번 더 수행 이때, 최단 거리 테이블이 갱신된다면 음수 간선이 존재하는 것 vs 다익스트라..

개념 정의: 그래프 구조에서 가장 짧은 경로를 찾는 알고리즘 다익스트라 알고리즘 개념 정의: 특정한 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산하는 알고리즘 최종적으로 각 노드까지의 최단 거리 정보가 저장 시간 복잡도: O(ElogV) : E - 간선 개수, V - 노드 개수 특징: 그리디 알고리즘: 매 상황에서 방문하지 않는 가장 비용이 적은 노드를 선택하여 반복 한 번 처리(방문)된 노드의 최단 거리는 고정 결과 각 노드까지의 최단 거리 정보가 저장 동작과정 간단 요약 출발 노드 설정 & 최단 거리 테이블 초기화 아래 과정 반복 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신 진행 흐름 // 노드의 개..