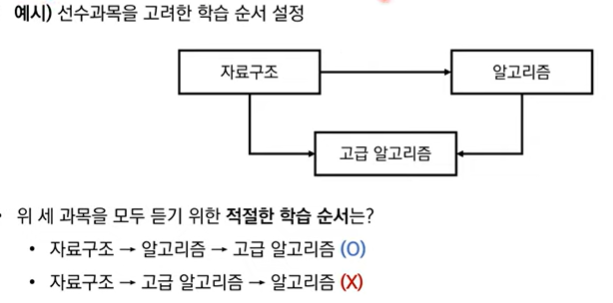
개념
- 정의: 사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스리지 않도록 순서대로 나열하는 것
- 즉, DAG(Direct Acyclic Graph): 순환하지 않는 방향 그래프에 대해서만 가능
- 시간 복잡도: O(V + E) - 노드 개수(V), 간선 개수(E)
- 동작과정 요약
- 진입차수가 0인 모든 노드를 큐에 삽입
- 큐가 빌 때까지 아래 과정 반복
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선 그래프에서 제거
- 새롭게 집입차수가 0이 된 노드를 큐에 삽입
- 최종적으로 각 노드가 큐에 들어온 순서가 위상 정렬을 수행한 결과
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재
그래프 기본 개념
- 집입차수(Indegree): 특정 노드로 들어오는 간선 개수
- 진출차수(Outdegree): 특정 노드에서 나가는 간선 개수

진행 흐름
0. 방향 그래프 및 진입 차수 테이블 준비
- 노드의 개수만큼 진입 차수 테이블 준비
- 방향 그래프를 받을 2차원 테이블 준비
- 방향 그래프에 간선이 추가될 때마다 진입 차수 테이블 증가 시키기
코드
// 진입 차수 테이블 초기화(0)
int[] indegree = new int[v+1];
// 방향 그래프 초기화
ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i <= v; i++) {
graph.add(new ArrayList<Integer>());
}
// 방향 그래프의 모든 간선 정보를 입력 받기
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph.get(a).add(b); // 정점 A에서 B로 이동 가능
// 진입 차수를 1 증가
indegree[b] += 1;
}
1. 진입차수가 0인 모든 노드를 큐에 삽입
코드
// 1. 진입차수가 0인 노드를 큐에 삽입
Queue<Integer> q = new LinkedList<>();
for (int i = 1; i <= v; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
작동 방식

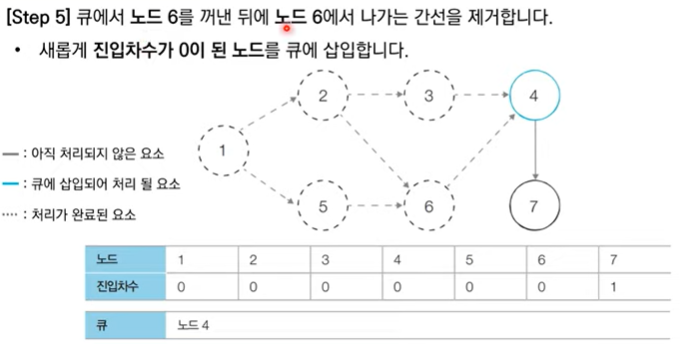
2. 큐가 빌 때까지 반복
큐에서 나온 순서 = 위상 정렬 순서
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선 그래프에서 제거
- 새롭게 집입차수가 0이 된 노드를 큐에 삽입
코드
// 2. 큐가 빌때까지 반복
ArrayList<Integer> result = new ArrayList<>(); // 위상정렬 결과 리스트
while (!q.isEmpty()) {
int now = q.poll();
result.add(now);
// 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for (int i = 0; i < graph.get(now).size(); i++) {
indegree[graph.get(now).get(i)] -= 1;
// 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if (indegree[graph.get(now).get(i)] == 0) {
q.offer(graph.get(now).get(i));
}
}
}
작동 방식






3. 위상 정렬 결과 출력
코드
//3. 위상 정렬 결과 출력
for (int i = 0; i < result.size(); i++) {
System.out.print(result.get(i) + " ");
}
작동 방식

전체 코드
public class struct {
public static void main(String[] args) throws IOException {
//1. 가중치 그래프 생성 & 진입차수 테이블 생성
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
ArrayList<ArrayList<Integer>> graphs = new ArrayList<>();
for(int i=0; i<=n; i++){
graphs.add(new ArrayList<>());
}
int[] degrees = new int[n+1];
// 모든 간선 정보를 입력받기
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graphs.get(a).add(b);
degrees[b]++; //진입 차수 테이블 갱신
}
//2. 진입차수가 0인 모든 노드 큐에 삽입
Queue<Integer> q = new LinkedList<>();
for(int i=1; i<=n; i++){
if(degrees[i] == 0){
q.offer(i);
}
}
//3. 큐가 빌때까지 아래 과정 반복
ArrayList<Integer> result = new ArrayList<>();
while(!q.isEmpty()){
int now = q.poll();
result.add(now);
//큐의 원소와 연결된 노드의 진입차수 -1
for(int next : graphs.get(now)){
degrees[next] -= 1;
//새롭게 진입차수가 0이 된 노드를 큐에 삽입
if(degrees[next] <= 0) {
q.offer(next);
}
}
}
//4. 결과 출력
System.out.println(result.toString());
}
}
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| 14. 그래프 - 트리(Tree), 이진 탐색 트리(BST), 트리 순회(Tree Traversal) (2) | 2024.04.02 |
|---|---|
| 13. 그래프 - 최소 공통 조상(LCA) (0) | 2024.04.02 |
| 11. 그래프 - 무방향 그래프 사이클 판별, 최소 신장 트리 (0) | 2024.04.02 |
| 10-2. 그래프 - 음수 간선의 최단 거리 - 벨만 포드 알고리즘 (0) | 2024.04.02 |
| 10. 그래프 - 최단 경로 알고리즘(다익스트라, 플로이드 워셜) (0) | 2024.04.02 |