스택 (Stack)
- 정의: 스택은 LIFO (Last In, First Out) 방식으로 작동하는 자료구조
- 즉, 가장 나중에 삽입된 데이터가 가장 먼저 꺼내짐
- 목적: 스택은 재귀적인 알고리즘, 계산기 구현, 함수 호출 관리 등에 자주 사용
- 주요 연산
- push(): 스택의 맨 위에 요소를 추가 - O(1)
- pop(): 스택의 맨 위 요소를 제거하고 반환 - O(1)
- peek(): 스택의 맨 위 요소를 제거하지 않고 반환 - O(1)
- isEmpty(): 스택이 비었는지 확인
자바 코드 예시
import java.util.Stack;
Stack<Integer> stack = new Stack<>();
// push 연산
stack.push(10);
stack.push(20);
stack.push(30);
// peek 연산
System.out.println("Top element: " + stack.peek()); // 30
// pop 연산
System.out.println("Popped element: " + stack.pop()); // 30
// isEmpty 연산
if(stack.isEmpty()) {
System.out.println("Stack is empty.");
} else {
System.out.println("Stack is not empty.");
}
큐 (Queue)
- 정의: 큐는 FIFO (First In, First Out) 방식으로 작동하는 자료구조
- 즉, 먼저 삽입된 데이터가 먼저 꺼내짐
- 목적: 큐는 작업 대기열, 프로세스 스케줄링, 네트워크 요청 관리 등에 사용
- 주요 연산
- offer() / add(): 큐의 뒤에 요소를 추가 - O(1)
- poll() / remove(): 큐의 앞에 있는 요소를 제거하고 반환 - O(1)
- peek(): 큐의 앞에 있는 요소를 제거하지 않고 반환 - O(1)
- isEmpty(): 큐가 비었는지 확인
자바 코드 예시
import java.util.LinkedList;
import java.util.Queue;
Queue<Integer> queue = new LinkedList<>();
// offer 연산
queue.offer(10);
queue.offer(20);
queue.offer(30);
// peek 연산
System.out.println("Front element: " + queue.peek()); // 10
// poll 연산
System.out.println("Polled element: " + queue.poll()); // 10
// isEmpty 연산
if(queue.isEmpty()) {
System.out.println("Queue is empty.");
} else {
System.out.println("Queue is not empty.");
}
링크드 리스트 (Linked List)
- 정의: 링크드 리스트는 노드들이 포인터로 연결된 선형 자료구조
- 각 노드는 데이터와 다음 노드를 가리키는 포인터를 포함
- 목적: 배열과 달리, 링크드 리스트는 동적으로 크기를 변경할 수 있으며, 삽입/삭제가 용이
- 주요 연산
- add(): 리스트의 끝에 요소를 추가 - O(1)
- add(index, element): 지정한 위치에 요소를 삽입 - O(n) ( 특정 인덱스 찾기 )
- remove(): 특정 위치의 요소를 제거 - O(1) or O(n)
- get(): 특정 위치의 요소를 반환 - O(n)
- size(): 리스트의 크기를 반환
자바 코드 예시
import java.util.LinkedList;
LinkedList<Integer> linkedList = new LinkedList<>();
// add 연산
linkedList.add(10);
linkedList.add(20);
linkedList.add(30);
// get 연산
System.out.println("Element at index 1: " + linkedList.get(1)); // 20
// remove 연산
linkedList.remove(2); // 30 삭제
// size 연산
System.out.println("Size of linked list: " + linkedList.size()); // 2
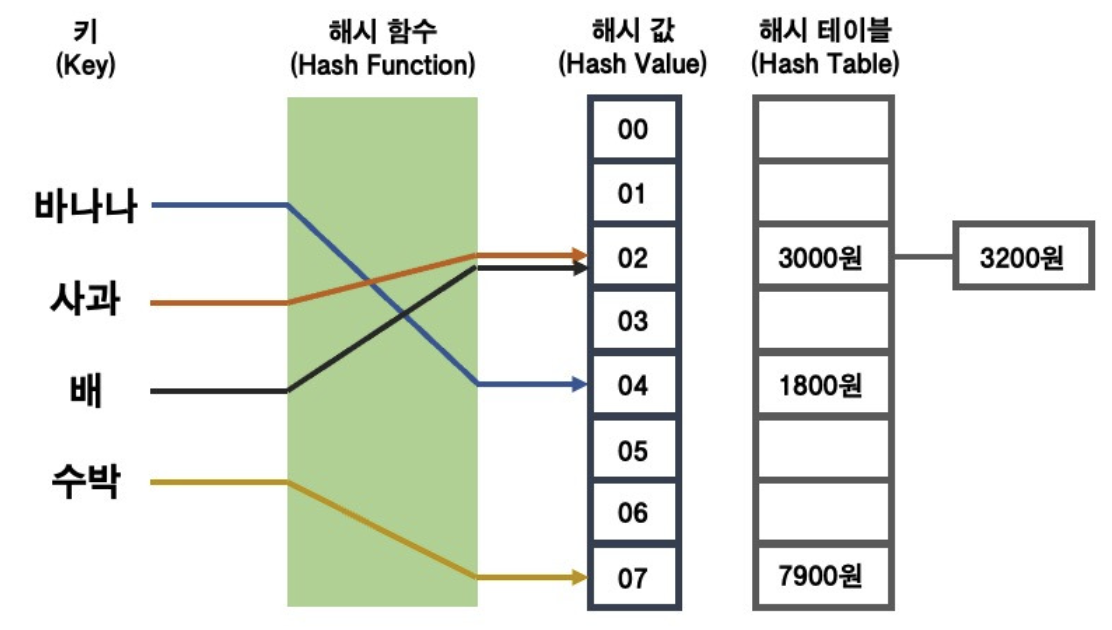
해시테이블 (Hash Table)
- 정의: 해시테이블은 키(key)와 값(value)을 매핑하는 자료구조로, 데이터의 효율적인 검색과 삽입을 위해 해시 함수를 사용
- 해시 함수란?: 키를 입력으로 받아 고유한 인덱스를 반환하여, 값을 해당 인덱스에 저장
- 목적: 해시테이블은 빠른 데이터 검색과 저장을 위해 사용
- 주로 데이터베이스 인덱스, 캐싱 시스템, 중복 검사 및 연관 배열 구현에 사용
- 주요 연산
- put(key, value): 해시 함수로 계산된 인덱스에 값을 저장. - O(1) 최악의 경우 O(n)
- get(key): 주어진 키에 해당하는 값을 반환. - O(1) 최악의 경우 O(n)
- remove(key): 주어진 키에 해당하는 값을 삭제. - O(1) 최악의 경우 O(n)
- containsKey(key): 특정 키가 존재하는지 확인.
- containsValue(value): 특정 값이 존재하는지 확인.
자바 코드 예시
import java.util.HashMap;
// put 연산
hashTable.put("apple", 1);
hashTable.put("banana", 2);
hashTable.put("cherry", 3);
// get 연산
System.out.println("Value for 'apple': " + hashTable.get("apple")); // 1
// remove 연산
hashTable.remove("banana");
// containsKey 연산
if (hashTable.containsKey("banana")) {
System.out.println("Banana is in the hash table.");
} else {
System.out.println("Banana is not in the hash table.");
}
해시 함수
- 나눗셈 방법 (Division Method)
- 해시 값 = 키 % 테이블 크기
- 가장 간단한 방식으로, 테이블 크기가 소수일 때 더 효율적으로 작동
- 곱셈 방법 (Multiplication Method)
- 해시 값 = ⌊테이블 크기 * (키 * A % 1)⌋ ( A는 0과 1 사이의 상수 )
- 나눗셈 방법보다 충돌이 적고, 테이블 크기가 2의 거듭제곱일 때 효율적
- SHA, MD5 같은 암호학적 해시 함수
- 데이터를 블록 단위로 나누고, 각 블록에 반복적인 수학적 연산을 적용해서, 마지막에 고정된 비트 수로 변환
- 암호학적 해시 함수는 일반적인 해시 테이블보다는 보안과 관련된 시스템에서 주로 사용
해시 충돌 해결 방법
- 해시테이블은 키를 해시 함수로 변환하여 고유한 인덱스에 값을 저장하지만, 서로 다른 키가 동일한 인덱스를 가리키는 경우, 이를 해시 충돌이라고 함
- 이를 해결하기 위한 여러 가지 방법이 존재
1. 체이닝 (Chaining)
- 정의: 체이닝은 해시 충돌이 발생했을 때, 같은 해시 인덱스를 갖는 여러 데이터를 링크드 리스트로 연결하는 방식
- 충돌이 발생하면 해당 인덱스에 새로운 노드를 추가하는 식으로 해결합니다.
- 장점
- 충돌이 많은 경우에도 데이터를 유연하게 저장할 수 있음.
- 테이블의 크기에 크게 의존하지 않음.
- 단점
- 충돌이 많이 발생하면 검색 속도가 느려질 수 있음 (최악의 경우 O(n))
2. 개방 주소법 (Open Addressing)
- 정의: 해시 충돌이 발생할 경우, 해시테이블 내에서 다른 빈 슬롯을 찾아 데이터를 저장하는 방법
- 선형 탐사 (Linear Probing): 고정된 간격으로 다음 슬롯을 찾는 방식 (
index + 1, index + 2, ...)- 클러스터링 문제가 발생할 수 있음
- 이차 탐사 (Quadratic Probing): 거리가 제곱수로 증가하는 방식으로 다음 슬롯을 찾는 방식 (
index + 1^2, index + 2^2, ...)- 클러스터링 문제를 줄일 수 있지만, 테이블이 꽉 차면 효율이 떨어질 수 있음
- 이중 해싱 (Double Hashing): 두 개의 해시 함수를 사용해 충돌 시 다른 해시 값으로 이동
- 클러스터링 문제를 효과적으로 방지 가능
- 선형 탐사 (Linear Probing): 고정된 간격으로 다음 슬롯을 찾는 방식 (
- 장점
- 별도의 추가 자료구조(예: 링크드 리스트)가 필요하지 않음
- 메모리 사용 효율성이 높음
- 단점
- 해시테이블이 꽉 차면 성능이 저하될 수 있음
- 삭제 연산이 복잡할 수 있음

+ 클러스터링 문제
- 정의: 해시 충돌이 발생했을 때, 특정 영역에 데이터가 밀집되어 해시 테이블 성능이 저하되는 현상
- 선형 탐사에서 클러스터링 문제가 발생하는 이유
- 선형 탐사는 충돌이 발생할 경우, 연속적인 인덱스(예: i+1, i+2, i+3...)를 탐색하며 빈 공간을 찾음
- 결과적으로, 데이터가 인접한 연속적인 인덱스에 저장되기 쉬움
- 새로운 충돌이 발생할 때, 이미 생성된 데이터 밀집 구간(클러스터)로 인해 더 많은 충돌이 발생하게 되고, 데이터가 점점 한 곳에 몰리게 되는 문제가 발생
- 이차 탐사에서 클러스터링 문제가 완화되는 이유
- 이차 탐사는 제곱 단위로 탐색 범위를 늘리므로, 탐색 위치가 선형 탐사처럼 연속적이지 않고, 보다 넓게 퍼짐