개념
- 정의: 리스트에 순차적으로 접근할 때, 2개의 포인터로 알고리즘 시간 복잡도를 최적화 하는 방법
- 시간 복잡도: O(n)
- 단, 정렬이 된 상태여야만 사용 가능하기에 정렬이 필요한 경우 O(nlogn)
언제 사용?
기준값(N)을 만드는 두 수의 조합
- 기준값(N)을 만들 수 있는 두 수의 조합의 경우의 수
int[] A = new int[n];//정렬된 배열
int M; //기준값
//투 포인터 선언
int s_index = 0;
int e_index = n-1;
//결과 경우 수 저장
int count = 0;
while(s_index < e_index){
//기준값 보다 작은 경우
if(A[s_index] + A[e_index] < M){
s_index++;
}
//기준값 보다 큰 경우
else if(A[s_index] + A[e_index] > M){
e_index--;
}
//기준값인 경우
else{
count++;
e_index--;
}
}
연속된 자연수의 합의 모든 경우 구하기
기준값(N)과 현재까지 값(sum) 이 있을때,
1. sum < N이면,
- end_index++;
- sum += end_index;
2. sum > N이면,
- sum -= start_index;
- start_index++;
3. sum == N이면,
- count++
- end_index++;
- sum += end_index;
특정한 합을 가지는 부분 연속 수열 찾기
- 정의: n개의 자연수로 구성된 수열에서, 합이 M인 부분 연속 수열의 개수를 구하는 문제
- 시간 복잡도: O(N)
- 동작과정
- 시작점(start)와 끝점(end)위치를 첫 번째 인덱스로 초기화
- 모든 경우를 확인할 때 까지 아래 과정 반복
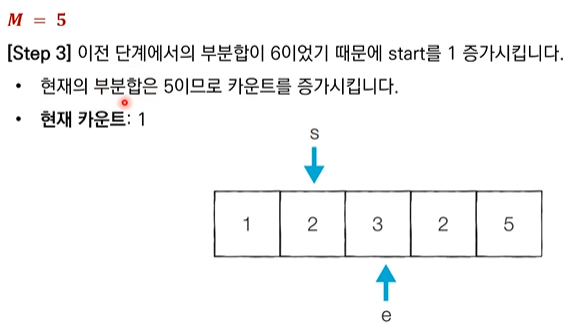
- 현재 부분 합이 M과 동일 - 카운트 & start를 1 증가
- 현재 부분 합이 M보다 작음 - end를 1 증가 (부분 합을 증가 시킴)
- 현재 부분 합이 M보다 큼 - start를 1증가 (부분 합을 감소 시킴)








코드
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); //데이터의 개수 N// int
int m = sc.nextInt(); //찾고하 하는 부분합 M
int[] arr = new int[n]; //전체 수열
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
}
//부분 수열 개수, 부분합, 끝(end)
int cnt = 0, intervalSum = 0, end = 0;
for(int start = 0; start < n; start++){
//부분 합이 기준(m)보다 커질때까지 end값 이동
while(intervalSum < m && end < n){
intervalSum += arr[end];
end += 1;
}
//end값이 이동 완료되었을때, 부분합이 기준(m)과 동일한지 확인
if(intervalSum == m){
cnt += 1;
}
//부분합이 기준(m)이상이기에, 다음 시작(start)값으로 이동
intervalSum -= arr[start];
}
//결과 출력
System.out.println(cnt);
}
}
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| 8. 구간합 (0) | 2024.04.02 |
|---|---|
| 7-2. 슬라이딩 윈도우 (0) | 2024.04.02 |
| 6. 소수 판별 (0) | 2024.04.02 |
| 5. 다이나믹 프로그래밍(동적 계획법) (0) | 2024.02.26 |
| 4. 탐색 알고리즘(순차, 이진 탐색) (0) | 2024.02.22 |